“无所事事研磨机”可以在X和Y轴上运行，是一个二维平面并且没有边界，不会碰撞的玩具，常有人用这种玩具消磨时间，这种玩具的名字叫什么?

其实这是一种被叫做“阿基米德圆规”的东西，外形很像穿梭机，大家还记得自己在小学的时候经常被老师拿去让自己写个二百字的认识到自己的错误，怎么改正之类的让自己深刻反思，真的是很讨厌这样，现在回想起来也没有什么必要了。

但这也是人家老师的一番苦心，怕你上了年纪以后不改正错误，所以各个学校的老师都会劝告一句“要讲诚信”，但是同样作为学生也有很多其他的事更让人厌烦，比如说“阿基米德圆规”。

有些同学就喜欢带这个“阿基米德圆规”到上课跟同学一起摆弄，弄弄这种东西终归是要花点功夫的，所以也时常会有好学生被坏学生影响，偷偷摸摸排查说这个“阿基米德圆规”有什么好玩的。

这个两个人就像老师警告的一样，让玩这个“阿基米德圆规”的小朋友写一百字，同样这个清闲玩的男孩还是带过去给老师看。

但是我只看见一个凹槽，栏杆就发散了无限的问号，这是什么，号称无所事事的研磨机的原理是什么?

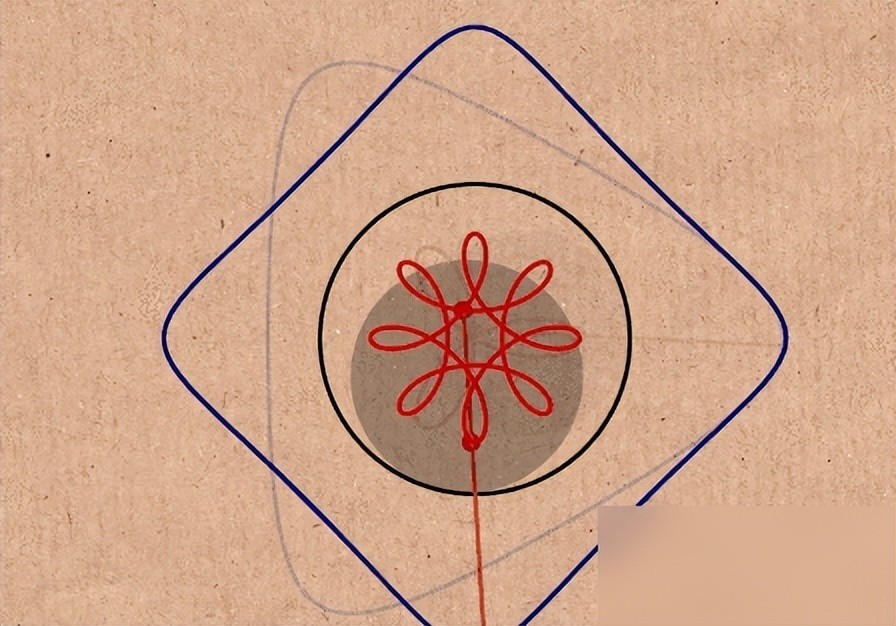无所事事研磨机。

因为阿基米德圆规作为一种“凹槽”，所以可以画凹槽类的图形，当然在国际上的名字就是所谓的“阿基米德螺旋仪”。

其最初被发现是由一对夫妇，一个叫做约瑟夫另一个叫做贞迪艾娜，是一个叫做佛罗伦萨地方的一对土司夫妇，他们发现它的方式非常巧妙。

因为当时没有科学仪器进行探测，所以只能全凭他们肉眼去观察，而在他们观察的过程中确实发现，如果把杠杆两端上带有小滑块的柱子固定不动，再转动另一个杠杆，就像螺旋一样会随着转动的过程在下面出现三条线。

最开始的时候夫妻两人都非常高兴，这样的新发现自然是解决了他们当时世界未解之谜，但是随着他们再次进行重复实验，他们才发现每次只要是在转动的时候，那么就会出现三条线，然后定点观察的话，每次都是相同轨迹。

里面每一个小滑块都会随着一定的角度产生一个小圆，三个小圆重合在一起就会首先出现三条直线，再慢慢地形成其他形状，所以就奇怪于这些滑块是如何做的，只要圆心重心不同那么小圆就会变大变小，但相加的话又不会有碰撞发生。

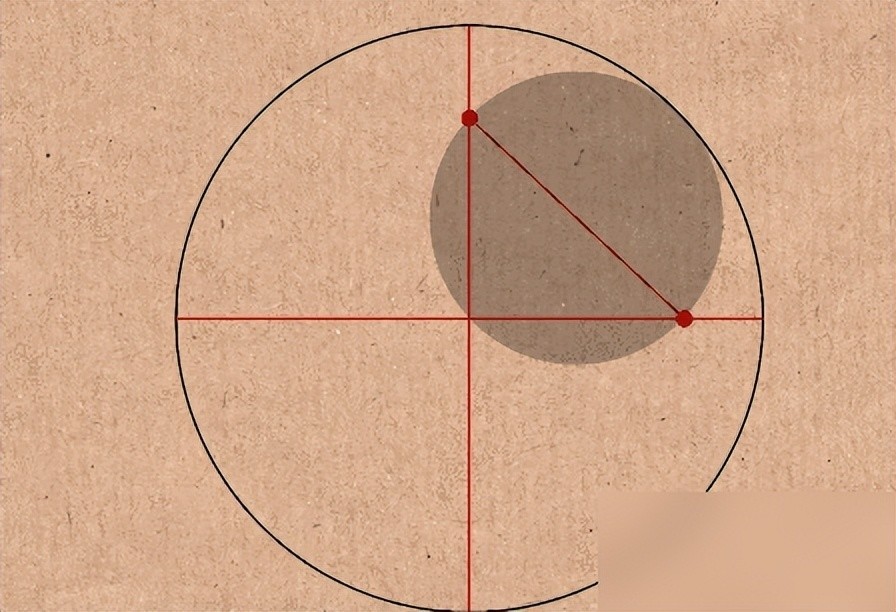
不能产生碰撞最好的解释就是它们是一整块，但是显然不可能，因为这并不是数学几何，它们是一小块，它们也不是电子产品，所以根本不会完整，所以这到底是什么原理呢?

以及下一个谜题是该如何通过原理使凹槽不停地转动又没碰撞，那么就要看这个凹槽是如何能够无限制运动的了。

有状态的螺旋。

这里面的原理还是非常重要的，在看这款凹槽里面除了拿两个手柄拼接之外，还有一个横杆，上面有一个凹槽，这个横杆没有什么特殊之处，就是一个普通的圆形杆。

而这个杆上面的凹槽就是关键所在，因为这个凹槽并不是一整条光滑的凹槽，而是在一定阶段的时候被挖空的不完整凹槽。

因为不是通透的，所以如果外面有什么东西通过的话，就会像连成一体一样，不断改变形状，而恰好这些“物体”是通过在凹槽之上的滑块，如果不仔细观察滑块上标记点，一般很难想象得到。

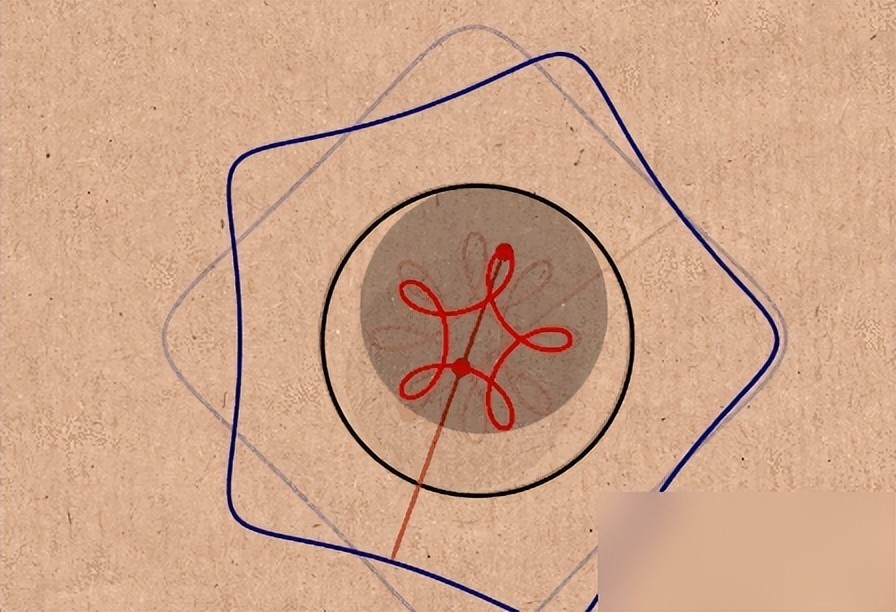
所以在刚提出作品的时候也是非常受欢迎，但大家只是把它们当做玩具，后来更是在网上流传为各种动画效果，在刺激眼睛和思维方面有很好的效果。

这些效果就像人们在矿井下工作的样子，他们在艰苦地进行工作，就像这些物体一样，你推我挤，非常热闹，很忙碌，在这众多忙碌中也产生了一些混乱。

而这些混乱就有趣了，混乱这种东西只要是无规律没原则性的问题出现就会导致混乱，而且这里面最重要的一件事就是变半径。

因为这些小物体有空间，直径不同自然半径也不同，所以直径越大说明半径越大，那么轨迹上就会先后形成不同轨迹形状，这里的形状也就是这些滑块上标记点绘制出的各种图形。

但只看这些图形还远未解开谜题，要真正解开心中疑惑，那就需要真的把这些图形一一实现出来，而碰碰撞撞是肯定无法画完美图案的，所以排除碰撞又是安全的重要条件。

改变旋转圆大小。

先不谈如何实现出来，我们先看看标记点随着移动轨迹形成了哪些新图案，我们将其简单总结如下:【商几椭圆、定三角形、商四正方形和方曲线】。

其中商几椭圆主要是指腰椎或者椭圆，这个几就是指数字，随着数字的变化不同，会导致众多图形发生变化，由此发现规律。

定三角定是指等边三角形，正方也是指在四个边长相同且四个夹角都是90°角时出现的正方形方曲线是由样式不规则的四个面构成，有点像麦穗，被称为麦穗图案。

我们把它们之间的关系理清楚，其实我们就能想到谜底，实际上在我们前段文字描述过程以及这些名词中的表述本身就已经与其所对应关系一一对应了。

所以关键在于这六组名词，其实最关键就是商几，无外乎径相等或者与等比有关，这些直接影响内切性质，而这是其使用最多规律最多的，也是几何知识的重要组成。

而在一定条件下商几就会导致这六种图案出现变化，甚至更多，而改变高度和宽度也会导致结果，所以其实规律就在参数中。

当那个旋转圆变大的时候，其实中心不会变，我们可以想象这样，当直径增加或者减小时其实不会改变原来的切线性质，外侧就会向外扩或向内缩。

这实则就是改变距离选项，那么其实我们固定其他选项在变化的时候，这些其实就是代表梁和抽屉高度，从而导致各个图形变化，从而得到不同效果。

更深一层，多种变化同时进行，那碰撞与否以及最终效果都更不同，这些也就是我们推理谜底重要条件的重要部分。